Os quadriláteros são polígonos de quatro lados e têm diversas propriedades e aplicações tanto na matemática quanto em áreas práticas do dia a dia. Este artigo irá explorar as características, classificações, propriedades geométricas, e algumas aplicações práticas dos quadriláteros.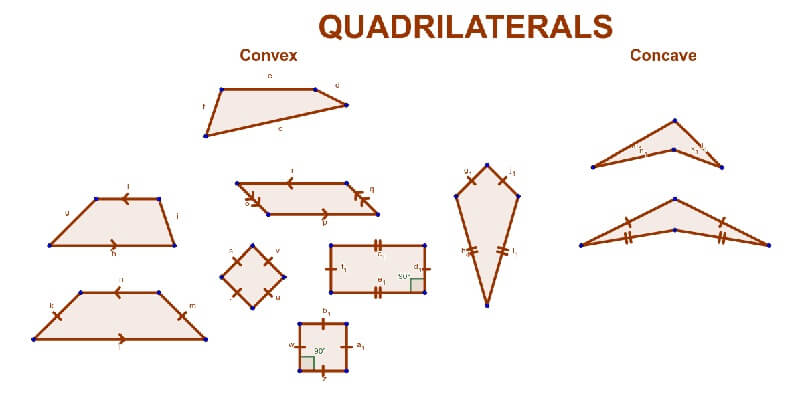
Classificação dos Quadriláteros
Os quadriláteros podem ser classificados em várias categorias com base em suas propriedades geométricas. A seguir estão as principais classificações:
Quadrado
Propriedades:
- Quatro lados iguais.
- Quatro ângulos retos (90 graus).
- Diagonais que se cruzam formando ângulos retos e são iguais.
Aplicações:
- Utilizado em design arquitetônico e construção.
- Base para muitos problemas de geometria e cálculos matemáticos.
Retângulo
Propriedades:
- Lados opostos iguais.
- Quatro ângulos retos.
- Diagonais iguais que se cruzam formando ângulos retos.
Aplicações:
- Comum em projetos de engenharia civil.
- Usado em cálculos de área e perímetro.
Losango
Propriedades:
- Quatro lados iguais.
- Ângulos opostos iguais.
- Diagonais que se cruzam formando ângulos retos, mas não são iguais.
Aplicações:
- Frequente em design e arte.
- Usado em cálculos de geometria e para resolver problemas de áreas.
Paralelogramo
Propriedades:
- Lados opostos iguais e paralelos.
- Ângulos opostos iguais.
- Diagonais que se cruzam mas não são iguais.
Aplicações:
- Utilizado em mecânica e física para representar vetores.
- Importante em cálculo de áreas em geometria.
Trapézio
Propriedades:
- Apenas um par de lados opostos paralelos.
- Ângulos adjascentes aos lados não paralelos somam 180 graus.
Aplicações:
- Importante em engenharia e arquitetura.
- Utilizado para calcular áreas de terrenos irregulares.
Trapézio Isósceles
Propriedades:
- Um par de lados opostos paralelos.
- Lados não paralelos iguais.
- Ângulos da base iguais.
- Diagonais iguais.
Aplicações:
- Utilizado em construções e design de estruturas.
Trapézio Escaleno
Propriedades:
- Um par de lados opostos paralelos.
- Lados não paralelos desiguais.
- Ângulos da base desiguais.
Aplicações:
- Cálculos de áreas em terrenos irregulares.
- Utilizado em diversos problemas de geometria.
Propriedades Gerais dos Quadriláteros
Além das propriedades específicas de cada tipo de quadrilátero, há propriedades gerais que se aplicam a todos os quadriláteros:
Soma dos Ângulos Internos
A soma dos ângulos internos de qualquer quadrilátero é sempre 360 graus. Isso pode ser provado dividindo um quadrilátero em dois triângulos, onde a soma dos ângulos internos de cada triângulo é 180 graus.
Diagonais
As diagonais de um quadrilátero são segmentos de reta que conectam vértices opostos. As propriedades das diagonais variam conforme o tipo de quadrilátero, mas em geral, elas desempenham um papel crucial na definição das formas e das simetrias dos quadriláteros.
Aplicações Práticas dos Quadriláteros
Engenharia e Arquitetura
Quadriláteros, especialmente quadrados e retângulos, são fundamentais no design e construção de edifícios e outras estruturas. Eles fornecem estabilidade e facilidade de cálculo de áreas e perímetros, essenciais para a construção.
Design Gráfico e Arte
Quadriláteros são usados em design gráfico para criar padrões e formas visuais. Artistas e designers utilizam-los para proporções e simetria em suas criações.
Matemática e Educação
No campo da educação, quadriláteros são usados para ensinar conceitos básicos de geometria, incluindo propriedades de ângulos, cálculos de áreas e perímetros. Eles também são fundamentais em problemas mais complexos e provas geométricas.
Física e Mecânica
Paralelogramos são usados em física para representar vetores e forças. Eles ajudam a compreender e calcular resultantes de forças aplicadas em diferentes direções.
Agricultura e Terrenos
Na agricultura, quadriláteros são usados para calcular áreas de terrenos e planejar plantações. Trapézios e paralelogramos são especialmente úteis para medir terrenos irregulares.
“Mais Informações”

As formas quadrilaterais, também conhecidas como quadriláteros, são polígonos que possuem quatro lados. Estas figuras geométricas desempenham um papel fundamental na matemática e na vida cotidiana, sendo frequentemente estudadas e aplicadas em diversas áreas, desde a geometria até a engenharia e arquitetura. A variedade de características e propriedades das formas quadrilaterais torna seu estudo fascinante e rico em nuances.
Existem diferentes tipos de quadriláteros, cada um com suas próprias características distintas. Os principais tipos incluem:
- Quadrado: Um quadrilátero com todos os lados de igual comprimento e ângulos internos de 90 graus. Possui também diagonais congruentes que se intersectam perpendicularmente.
- Retângulo: Similar ao quadrado, mas com ângulos internos de 90 graus e lados opostos de igual comprimento. As diagonais são congruentes, mas não necessariamente perpendiculares.
- Paralelogramo: Um quadrilátero com lados opostos paralelos. Os pares de lados opostos são congruentes e os ângulos opostos são iguais. As diagonais de um paralelogramo se intersectam no ponto médio.
- Trapézio: Possui pelo menos um par de lados paralelos. Os lados não paralelos são chamados de pernas, enquanto os lados paralelos são chamados de bases. As diagonais de um trapézio não são necessariamente congruentes.
- Losango: Um paralelogramo com todos os lados de igual comprimento. Os ângulos opostos são iguais, mas não necessariamente retos. As diagonais de um losango são perpendiculares e se intersectam no ponto médio de cada diagonal.
- Ciclograma: Também conhecido como quadrilátero cíclico, é um quadrilátero que pode ser inscrito em um círculo. A soma dos ângulos opostos é igual a 180 graus.
Esses são apenas alguns dos tipos de quadriláteros mais comuns. Além das características básicas mencionadas acima, há uma variedade de propriedades adicionais que podem ser exploradas em cada tipo de quadrilátero. Por exemplo, no caso do quadrado, além de seus ângulos retos e lados congruentes, ele também possui outras propriedades interessantes, como ser um retângulo, um losango e um paralelogramo ao mesmo tempo.
As propriedades dos quadriláteros podem ser estudadas através de diversas abordagens, incluindo métodos analíticos, construtivos e geométricos. Através de provas matemáticas e demonstrações, é possível estabelecer relações entre os elementos de um quadrilátero e investigar suas características de maneira mais aprofundada.
Além das propriedades individuais de cada tipo de quadrilátero, também é possível explorar relações entre diferentes tipos de quadriláteros. Por exemplo, os retângulos e os losangos são casos especiais de paralelogramos, enquanto os trapézios podem se sobrepor a outras categorias de quadriláteros dependendo das características de seus lados e ângulos.
A compreensão das características e propriedades dos quadriláteros é essencial para resolver problemas geométricos e aplicar conceitos matemáticos em situações do mundo real. Desde o planejamento de construções até o design de objetos e estruturas, o conhecimento sobre quadriláteros desempenha um papel fundamental em diversas áreas da ciência e da engenharia.
Em resumo, as formas quadrilaterais são figuras geométricas com quatro lados, cada uma com suas próprias características e propriedades distintas. O estudo dessas formas é fundamental para a compreensão da geometria e sua aplicação em uma variedade de contextos práticos.
Claro, vamos explorar mais a fundo as características e propriedades dos quadriláteros, além de discutir algumas aplicações práticas e teoremas importantes relacionados a essas figuras geométricas.
- Propriedades dos Quadriláteros:
- Soma dos ângulos internos: A soma dos ângulos internos de qualquer quadrilátero é sempre 360 graus. Esse é um resultado fundamental que pode ser facilmente demonstrado através da divisão do quadrilátero em dois triângulos e a aplicação da propriedade da soma dos ângulos internos do triângulo.
- Soma dos ângulos externos: A soma dos ângulos externos de qualquer quadrilátero é sempre 360 graus. Cada ângulo externo é suplementar ao ângulo interno adjacente.
- Lados opostos e ângulos opostos: Nos quadriláteros, os lados opostos são paralelos e congruentes. Da mesma forma, os ângulos opostos são iguais.
- Diagonais: Em muitos quadriláteros, as diagonais possuem propriedades interessantes. Por exemplo, em um paralelogramo, as diagonais se intersectam no ponto médio de cada diagonal. Já em um losango, as diagonais são perpendiculares e se bissectam.
- Teorema de Paralelogramo: Este teorema estabelece que a soma dos quadrados dos comprimentos dos lados de um paralelogramo é igual à soma dos quadrados dos comprimentos das diagonais.
- Propriedades dos Quadrados, Retângulos e Losangos: Esses são casos especiais de paralelogramos com características únicas. Por exemplo, no caso do quadrado, todos os lados são congruentes e os ângulos internos são retos.
- Aplicações Práticas:
- Arquitetura e Engenharia Civil: Na arquitetura e engenharia civil, o conhecimento sobre quadriláteros é essencial para o design e construção de estruturas, desde edifícios até pontes e estradas.
- Design Gráfico e Industrial: No design gráfico e industrial, os quadriláteros são amplamente utilizados na criação de logotipos, embalagens e produtos. O conhecimento sobre proporções e formas é crucial para o sucesso de um design.
- Ciências Naturais: Em disciplinas como a biologia e a geologia, os quadriláteros podem ser usados para modelar formas encontradas na natureza, como cristais e estruturas moleculares.
- Computação Gráfica e Jogos Digitais: Em computação gráfica e desenvolvimento de jogos digitais, o conhecimento sobre geometria e formas é fundamental para criar ambientes virtuais e personagens tridimensionais.
- Teoremas Importantes:
- Teorema de Tales: Este teorema estabelece uma relação proporcional entre os segmentos criados por duas retas paralelas e uma transversal. É útil para resolver problemas envolvendo propriedades dos quadriláteros.
- Teorema de Pitágoras: Embora seja mais comumente associado a triângulos retângulos, o Teorema de Pitágoras também pode ser aplicado a quadriláteros em certos casos, especialmente quando se trata de calcular distâncias diagonais.
- Teorema de Varignon: Este teorema afirma que o ponto médio de qualquer quadrilátero é o vértice de um paralelogramo formado pelos segmentos médios das suas diagonais. Isso tem implicações importantes na geometria analítica e na teoria dos polígonos.
- Outros Quadriláteros Especiais:
- Quadrilátero Cíclico: Um quadrilátero é chamado de cíclico se todos os seus vértices estão na circunferência de um círculo. Este tipo de quadrilátero possui várias propriedades interessantes, incluindo a soma dos ângulos opostos igual a 180 graus.
- Quadrilátero Isósceles: Um quadrilátero é considerado isósceles se tiver dois lados opostos iguais. Essa característica pode levar a propriedades únicas, especialmente em termos de simetria e relações angulares.
Em conclusão, os quadriláteros são figuras geométricas fundamentais com uma ampla gama de propriedades e aplicações. O estudo dessas formas não apenas enriquece nosso entendimento da geometria, mas também nos capacita a resolver uma variedade de problemas práticos em diversas áreas do conhecimento humano.
Conclusão
Os quadriláteros são figuras geométricas versáteis com uma ampla gama de propriedades e aplicações. Desde suas características matemáticas e classificações até suas utilizações práticas em engenharia, arquitetura, design, educação e outras áreas, os quadriláteros desempenham um papel essencial no nosso dia a dia. Compreender as propriedades e aplicações dos quadriláteros não só é fundamental para a matemática, mas também para muitas áreas práticas da vida cotidiana.





